Stack
Before going to the stack, we will read the enclosure of Abstract Data Types (ADT) extensively. What is ADT, what methods come in it and which stack is used? At the same time, we will also read and understand the functionality of each method of Abstract Data Types.
What is an Abstract Data Type (ADT)?
The abstract data type is a unique type of datatype. The abstract data type (ADT) is a mathematically specified entity that characterized a group or a set of its instances with A specific interface and A set of axioms.
An interface is a way to declare what a class is to do. It does not mention how to do it.
A collection of signatures of operations that can be invoked on an instance.
A set of axioms (preconditions and postconditions) that define the semantics of the operations i.e; what the operations do to instances of the ADT, but not how.
Let us see some operations of those mentioned ADT −
- Stack −
- isFull(), This is used to check whether or not the stack is full
- isEmpry(), Check if the stack is empty
- push(x), This helps to move x into the stack
- pop(), This deletes one item from the top of the stack
- peek(), This is used to get the topmost element
- size(), This function is used to store the number of elements
- Queue −
- isFull(), This is used to check whether the queue is full or not
- isEmpry(), This is used to check whether the queue is empty or not
- insert(x), At the rare end x will be added into the queue.
- delete(), This is used to delete one element from the front end of the queue
- size(), this function is used to get a number of elements present into the queue
- List −
- size(), this function is used to get and store a number of elements present into the list
- insert(x), add one element into the list
- remove(x), remove given element from the list
- get(i), this function is used to get the element at position i
- replace(x, y), this function is used to replace x with a y value
Why do we need to talk about ADTs in Data Structures?
The following points are appropriate as to why we need to talk about this :
- They serve as requirement specifications for the building blocks of algorithmic problem solutions.
- presents a language which facilitates and allows to communicate on a higher level of abstraction.
- ADT encapsulates data structures that indicate the organization of the data and the algorithm that implements them.
- Separate the issue of consistency and effectiveness.
Dynamic Sets
- We will deal with ADT instances of which are sets of some type of elements
-> Operations are provided that change the set - We call such class of ADTs dynamic set.
Method of Dynamic Set
Following are the dynamic set method :
- New( ) : ADT
- Insert ( S : ADT, v : element ) : ADT
- Delete ( S : ADT, v : element ) : ADT
- Isin ( S : ADT, v : element ) : boolean
-> New – for creation and construction
-> Insert and Delete – manipulation operations
-> Isin – access method
Axioms that define the methods
Following axioms show opetations behavior and functionality of these operations.
- Isin ( New ( ), v ) = false
- Isin ( Insert ( S, v ) , v) = true
- Isin ( Insert ( s, u ) , v ) = Isin ( s, v) , if v != u
- Isin ( Delete ( s, v ) , v ) = false
- Isin ( Delete ( s, u ) , v ) = Isin ( s, v ) , if v != u
Where s represent the dynamic set and v represent the element
Simple Dynamic Set Data Structures

- All stack and queue operations are Θ(1).
- List-Insert is Θ(1) for unsorted lists, O(n) for sorted lists
- List Delete is Θ(1) for doubly-linked lists, O(n) for singly-linked lis
if you don’t understant is than don’t worry go to asymptotic lectures. where all these thing is discussed in very details and advanced.
Stack
Stack is an ordered list where the new item is added and an existing element is deleted from only one end, called the top of the stack (TOS).
- A stack is a set of objects that are added and removed according to the concept of Last-in-first out (LIFO).
- objects can be inserted at any time, but only the last (i.e., the most currently inserted) object can be eliminated
- Inserting an element is known as pushing onto the stack. popping off the stack is synonymous with removing elements.
- Insert of an element onto the stack is called push or removing an element from stack is known as poping.
The Stack can be implemented in two ways:
The Static implementation uses arrays to create a stack. Static implementation though a very simple technique but is not a flexible way of creation, as the size of the stack has to be declared during program design, after that the size cannot be varied.
Dynamic implementation is also called linked list representation and uses pointers to implement the stack type of data structure.
stack is an ADT supporting four primary methods.
- new ( ) : ADT – Creates a new stack
- push ( S : ADT, O : element ) : ADT – Insert object O onto top of S
- pop ( S : ADT ) : ADT – Removes the top object of stack S, if the stack is empty an error occurs.
- top ( S : ADT) : element – Returns the top object of the stack, without removing it; if the stack is empty an error occurs.
- size ( S : ADT ) integer – Returns the number of objects in stack S
- isEmpty ( S : ADT ) : boolean – Indicates if stack S is empty.
pop removes the element but top tells about the element
Stack Can Help
- S can be easily computed if we know the closest day preceding i, on which the price is greater than the price on the day i. If this type of day exists, let’s call it h(i), otherwise, we conventionally define h(i) = -1
- In the above figure, h(0)= -1,h(1)=0, h(2)=1 h(3)=2, h(4)=3, h(5)=1 and h(6)=0
- The span is now computed as S = i – h(i)
- Example S5 = 5 – h(5) = 5 – 1 = 4
What to do with the Stack?
What are the possible values of h(7)?
Can it be 1 or 3 or 4?

by means of the definition of h(7) is the closes day procced it that’s the stack rate that is large than the rate on day 7. that day can’t be 1, three or four. So what are the feasible values of h(7) can take?
By showing the following pic we clearly told only 2,5, and 6 are the only possible values that h(7) can take.
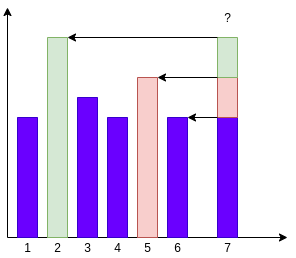
we save indices 2,5,6 within the stack. To determine h(7) we compare the price on day 7 with the price on day 6, day 5, day 2 in that order. first, we want to evaluate the rate on day 7 with price on day 6 if the price on day 7 is less than the price on day 6 than it is day 6 but suppose the price on day 7 became greater than price on day 6, then we are able to compare with price on day 5. if it is larger than the price on day five, then we will evaluate it with 2. if it is more than 2, then it is minus one that is h (7) = -1
2 will be at the bottom of the stack, 5 will be above that and 6 on the top of the stack
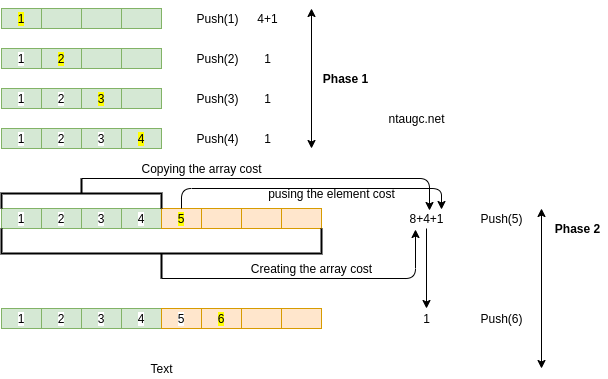
A Growable Array-Based Stack
Algorithm push(o)
if size() – N then A <- new array of length f(N)
for i <- 0 to N-1
A[i]<-S[i]
S<-A;t<-t+1
S[t] <- o
How large will be the new array?
There are two approach for growable stack:
- Tight Strategy: Add a constant amount to the old stack f(N) =N=c
- Growth Strategy: Double up f(N) = 2N
There are two operations to compare this strategy:
- A regular push operation: adds one element and costs one unit.
- A special push operation: create an array of size f(N), copy N elements, and add one element. Costs f(N)+N+1 units.
Tight Strategy
Let C = 4, start with an array of size 0 cost of a special push is 2N = 5

Performance of the Tight Strategy
- In phase i the array has size c*i
- Total cost of phase i is
c*i is the cost of creating the arry
c*(i-1) is the cost of copying elements into new array
c is the cost of the c pushes - Hence, cost of phase i is 2ci
- In each phase we do c pushes. Hence for n pushes we need n/c phases. Total cost of these n/c phases is
= 2c(1 + 2 + …..+n/c) ~ O(n^2/c)
Growth Strategy
Start with an array of size 0. cost of a special push is 3N + 1
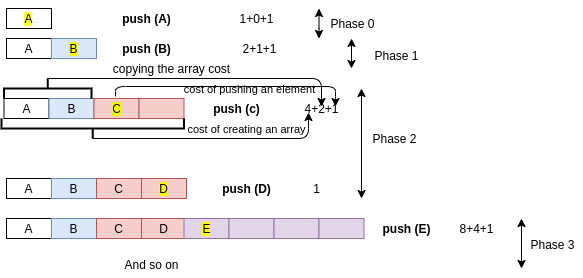
Performance of Growth Strategy
- In phase i the array has size 2^i
- The total cost of phase i is
2^i is the cost of creating the array
2^i-1 is the cost of copying elements into the new array
2^i-1 is the cost of the 2^i-1 pushes done in this phase - Hence, the cost of phase i is 2^i+1
- If we do n push, we will have log n phases
- The total cost of n pushes
= 2+4+8+ …. + 2^l(og n+1) = 4n-1
After comparing the performance of both ( Growth Strategy cost 4n-1 and Tight Strategy cost n^2/c) we can easily say Growth Strategy wins.
Summary
- Stack is a linear data structure.
- A Stack contains only a similar data type.
- In push ( ) we must have given an argument.
- In pop ( ) we don’t need an argument pop ( ) always remove top element.
- top ( ) function is also known as peek ( ).
- Reverse a string in programming and In computer science, Undo/Redo is a good example of the stack.